Ecuaciones y sistemas de ecuaciones
1) Define solución de una ecuación como un conjunto. ¿Qué es resolver una ecuación? ¿Cuándo se dice que una ecuación es equivalente a otra ecuación? En ese caso, ¿podemos decir que son ecuaciones equivalentes? ¿Qué son las transformaciones elementales sobre una ecuación? ¿Cómo se resuelve una ecuación?
2) Resuelve las siguientes ecuaciones:
3) ¿Qué es una ecuación diofántica? Pon un ejemplo.
Se llama "ecuación diofántica" a cualquier ecuación algebraica, de dos o más incógnitas, cuyos coeficientes recorren el conjunto de los números enteros, de las que se buscan soluciones enteras, esto significa, que pertenezcan al conjunto de los números
4) Resuelve la ecuación diofántica x2 + y2 = z2
5) Resuelve las siguientes ecuaciones:
* 2x + 3y - 1 =0 en el conjunto de los números enteros (ecuación diofántica).
* 2x + 3y - 1 =0 en el conjunto de los números racionales.
* 2x + 3y - 1 =0 en el conjunto de los números reales.
* 0x + 0y = 0
6) Clasifica y resuelve por el método de Gauss, en forma matricial, el sistema de ecuaciones lineales:
Sustituye la tercera ecuación por otra de forma que el sistema resultante sea compatible indeterminado uniparamétrico.
7) Dos albañiles hacen una reparación en 4 horas. Uno de ellos la haría en 6 horas. Calcula el tiempo que tardaría en hacerla el otro solo.
8) Halla el divisor de una división entera sabiendo que el dividendo es 595, que el cociente y el resto son iguales y que el divisor es el doble del cociente.
9) En una finca hay 22 árboles entre manzanos, ciruelos y perales. El doble del número de ciruelos más el triple del número de perales es igual al doble del número de manzanos. Halla el número de árboles de cada tipo si se sabe que el número de ciruelos es la mitad del de manzanos.
10) Clasifica y resuelve por el método de Gauss, en forma matricial, y gráficamente los siguientes sistemas de ecuaciones lineales:
btgrfhrth
























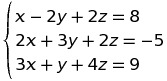






No hay comentarios:
Publicar un comentario